| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 함수
- Visual Studio
- Win32
- 문법
- 지식나눔강좌
- 리뷰
- 포인터
- Windows
- 알고리즘
- Direct2D
- 배열
- c
- Desktop
- Tips프로그래밍강좌
- Javascript
- CS
- 이지스퍼블리싱
- 백준
- Kotlin
- c#
- 연산자
- VS ERROR
- tipssoft
- c++
- 티스토리
- Tips강좌
- 프로그래밍
- 김성엽
- Programming
- doit코틀린프로그래밍
- Yesterday
- Today
- Total
F.R.I.D.A.Y.
BAEKJOON 1912:연속합(DP) 본문

주어진 배열에서 연속하는 각 요소의 합이 최대인 값 구하기.
코드
#include <iostream>
using namespace std;
#define max(x,y) ((x) > (y) ? (x) : (y))
int main() {
int n;
int* arr;
cin >> n;
arr = new int[n];
for (int i = 0; i < n; ++i) cin >> arr[i];
int result = arr[0];
{
for (int i = 1; i < n; ++i) {
if (arr[i - 1] > 0 && arr[i - 1] + arr[i] > 0) {
arr[i] += arr[i - 1];
}
result = max(arr[i], result);
}
}
cout << result;
delete[] arr;
return 0;
}
설명
일단 연속합이므로 n번째 요소까지의 합을 구할 때, i번째까지 더한 결과는 다음과 같다.
arr[i] = arr[i] + arr[i-1];그러나 모든 배열의 합을 구하는 것이 아니라, 연속하는 요소를 더해서 최대가 되는 값을 구하는 것이므로 위 점화식을 적용할 몇 개의 조건을 찾아야 한다.
값이 작아지는 경우는 더하려는 값이 음수인 경우이다. 다음 배열이 있다고 하자.

i = 0일 때 합은 1, i = 1일 때 합은 0이 된다. 즉, arr[0] arr[1]은 합을 구할때 이 둘의 합[# 합의 결과가 0]을 더하지 않더라도 결과에 문제가 되지 않는다. 이를 수식으로 변환하면 다음과 같다.
arr[0] + arr[1] > 0위 조건을 추가해 점화식을 적용하면 다음과 같아진다.
if(arr[i] + arr[i-1] > 0){
arr[i] += arr[i-1];
}이렇게만 코드를 구성하면 제대로된 값을 찾지 못한다. i - 1에 위치한 값이 음수인 경우를 생각해보자.
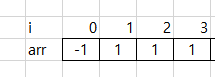
음수인 경우에도 위 코드대로 하면 arr[0] ar[1]의 합을 구한다. 여기에서 음수를 더해야할 필요가 있을까? 아니다. 오히려 최대를 구하는데 방해만 될 뿐이다. 즉, 하나의 조건이 추가되어야 한다.
arr[i - 1] > 0# 양수를 판단하는 것을 꼭 넣어야 하는가?
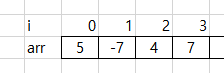
위와 같은 입력이 들어온다고 하자. arr[0] arr[1]의 합산은 -2이지만 그 결과를 arr[2]와 더했을 때는 0보다 큰 2가 된다. 여기에 arr[3]을 더하면 총 9가 되는데, 실제 위 입력에서 가장 큰 합산 수는 arr[2] + arr[3]인 11이 된다. 답을 찾을 수 없게 된다. 따라서 양수 판단에 대한 조건이 필수적이다.
위 조건을 합하면 다음과 같다.
for(int i = 1; i < n; ++i){
if(arr[i - 1] > 0 && arr[i] + arr[i - 1] > 0){
arr[i] += arr[i - 1];
}
}arr[0]을 초기 max값으로 두고, 이후 arr[i]와 max값을 비교해 더 큰 값을 max에 넣고 마지막에 max 값을 출력하는 것으로 문제를 해결할 수 있다.
# index
'DEV > Algorithm' 카테고리의 다른 글
| brute force VS. KMP algorithm (0) | 2025.04.07 |
|---|---|
| BAEKJOON 15649:N과 M(1) (0) | 2024.03.10 |
| BAEKJOON 1932:정수 삼각형(DP) (0) | 2021.12.21 |
| BAEKJOON 11053:가장 긴 증가하는 부분 수열 O(nLogn) for C++(DP) (0) | 2021.12.21 |
| BAEKJOON 11053:가장 긴 증가하는 부분 수열 O(n²) for C (0) | 2021.09.08 |



