| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 포인터
- 백준
- c++
- Tips프로그래밍강좌
- 리뷰
- Javascript
- 문법
- 티스토리
- Kotlin
- 프로그래밍
- tipssoft
- 이지스퍼블리싱
- Win32
- Visual Studio
- c
- 연산자
- 알고리즘
- Tips강좌
- 지식나눔강좌
- 김성엽
- doit코틀린프로그래밍
- Windows
- Direct2D
- 배열
- Desktop
- 함수
- CS
- VS ERROR
- c#
- Programming
Archives
- Yesterday
- Today
- Total
F.R.I.D.A.Y.
BAEKJOON 1932:정수 삼각형(DP) 본문
반응형

최대 합이 되는 경로 검색
1932번: 정수 삼각형
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net
코드
2차원 배열로 구성을 했다변 더 좋았겠지만, 2차원 배열을 굳이 사용하지 않더라도 수식만으로 2차원 배열을 사용하는 것처럼 구성이 가능하다는 것을 보이기 위해 1차원 배열을 사용해봤다.
#include <iostream>
using namespace std;
int main() {
int n;
cin >> n;
int* arr = new int[n * n];
cin >> arr[0];
for (int i = 1; i < n; ++i) {
cin >> arr[i * n];
arr[i * n] += arr[(i - 1) * n];
for (int k = 1; k < i; ++k) {
cin >> arr[i * n + k];
if (arr[(i - 1) * n + k - 1] > arr[(i - 1) * n + k])
arr[i * n + k] += arr[(i - 1) * n + k - 1];
else arr[i * n + k] += arr[(i - 1) * n + k];
}
cin >> arr[i * n + i];
arr[i * n + i] += arr[(i - 1) * n + i - 1];
}
int max = arr[(n - 1) * n];
for (int i = 1; i < n; ++i) {
if (max < arr[(n - 1) * n + i]) {
max = arr[(n - 1) * n + i];
}
}
cout << max;
delete[] arr;
return 0;
}
설명
문제의 설명에 따라 i+1층의 계산 결과는 i층의 좌우측 값을 선택적으로 더해 구성할 수 있다.
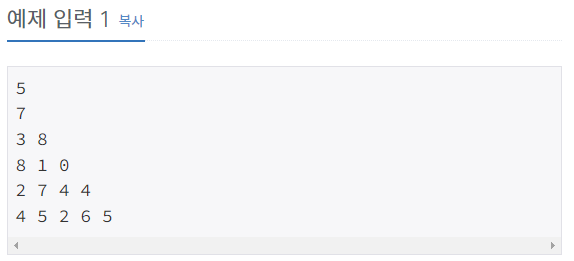

DP는 큰 문제를 작게 쪼개는 개념이니 만큼, 3층짜리 삼각형을 생각해보자.
각 배열의 시작과 끝({7}, {3, 8}, {8, 0})는 더할 수 있는 것이 정해져있다. 삼각형의 끝에 위치하기 때문이다.

그러나 밑줄이 그어지지 않은 1의 경우 바로 윗단의 3과 8을 더할 수 있다. 중요한 점은 어디를 더해야 더 큰 수가 나오느냐는 것인데, 1과 더했을 때 더 큰 수가 되는 값을 선택하면 된다. 3이 들어간 위치를 arr[1][i - 1], 8이 들어간 위치를 arr[1][i]이라 할 때, 우리는 arr[1][i]를 선택해야한다.
if(arr[1][i - 1] < arr[1][i]){
arr[2][i] += arr[1][i];
}else{
arr[2][i] += arr[1][i - 1];
}또한, (1)1 + 3과 (2)1 + 8에 동일한 값 n을 더했을 때 (1) < (2)는 언제나 참이다. 즉, (1)은 저장할 필요가 이후에 고려할 필요가 없다.
728x90
반응형
'DEV > Algorithm' 카테고리의 다른 글
| BAEKJOON 15649:N과 M(1) (0) | 2024.03.10 |
|---|---|
| BAEKJOON 1912:연속합(DP) (0) | 2021.12.21 |
| BAEKJOON 11053:가장 긴 증가하는 부분 수열 O(nLogn) for C++(DP) (0) | 2021.12.21 |
| BAEKJOON 11053:가장 긴 증가하는 부분 수열 O(n²) for C (0) | 2021.09.08 |
| BAEKJOON 2579: 계단 오르기 for C (0) | 2021.09.07 |
Comments




