| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 알고리즘
- 김성엽
- tipssoft
- 지식나눔강좌
- VS ERROR
- 티스토리
- 프로그래밍
- 문법
- 함수
- 리뷰
- 연산자
- 이지스퍼블리싱
- 배열
- Programming
- Direct2D
- doit코틀린프로그래밍
- c++
- Windows
- 백준
- c#
- Tips프로그래밍강좌
- CS
- Javascript
- Tips강좌
- Desktop
- Visual Studio
- 포인터
- Kotlin
- Win32
- c
- Yesterday
- Today
- Total
F.R.I.D.A.Y.
부동소수점 본문

실수를 표현하기 위해 C언어에서는 대표적으로 float와 double 자료형이 존재합니다. 이 자료형들이 어떻게 데이터를 가지고 해석하는지 알아봅니다.
실수를 표현하는 방법
우리 일상에는 나이, 날짜, 지폐와 같이 정수로 표현이 가능한 데이터가 존재합니다. 그러나 이것 외에도 키, 몸무게, 환율 등 실수로 표현해야 하는 데이터도 존재합니다. 정수는 이진수의 값을 올리면 된다지만, 0과 1로 표현되는 컴퓨터에서 실수는 단순히 값을 올리는 것으로만은 실수를 표현할 수 없습니다.
그렇다면 우리는 새로운 방법을 시도해볼 수 있습니다.
고정 소수점
특정 비트를 기준으로 한쪽 비트를 실수의 정수 영역을 저장하도록 하고, 반대쪽 비트는 실수의 소수점 영역을 저장하도록 하는 방법입니다.

4바이트, 즉 32비트 공간이 있다고 해봅시다. 그럼 상위 16개 비트(노란색)는 실수에서 정수 부분을, 하위 16개 비트(푸른색)는 소수점 영역을 담당하게 되는 것이죠.
이 방법은 이후에 소개할 부동 소수점 방식과 달리 오차가 존재하지 않습니다. 실수를 두 개의 정수로 분류해 처리하기 때문이죠.
그러나 두 개의 정수를 저장하는 만큼, 데이터의 범위가 굉장히 한정적입니다. 16비트에서 표현 가능한 데이터는 65,536개입니다. 심지어 정수 영역은 저장하는 값이 양수인지 음수인지 판별하기 위한 sign 비트를 가지고 있어야 합니다. 무엇이 되었던 어느 한쪽은 32,768개의 정수 중 하나만 담을 수 있게 됩니다. 더 큰 데이터를 담으려면 많은 메모리를 가지고 있어야 하죠.
부동 소수점
고정 소수점의 이러한 문제로 인해, 부동 소수점이라는 방식이 도입되었습니다. 값 자체를 저장하는 것이 아니라, 값을 도출할 수 있는 수식에 대한 정보를 저장하는 방식이라 생각하면 됩니다.
33.75
이 수를 이진수로 바꿔보겠습니다. 정수(소수점 왼쪽 값) 부분은 십진수를 이진수로 바꾸는 방식을 그대로 이용하면 됩니다. 소수(소수점 오른쪽 값)는 아래와 같은 방식을 취합니다.
| 연산 | 결과 | 비트값 |
| 0.75 * 2 | 1.5 | 1 |
| 0.5 * 2 | 1.0 | 1 |
| 0 * 2 | 0.0 | 0 |
먼저 소수에 2를 곱합니다. 곱한 값이 정수가 존재할 경우 그 자릿수는 1이 되고 정수를 지웁니다. 연산 결과로 남은 소수에 다시 2를 곱하고 이전 과정을 되풀이하면 이진수로 바꿀 수 있습니다.
이 과정으로 33.75는 다음처럼 변경됩니다.
10 0001.11₂[# 이진수]
이 값은 다시 아래와 같이 변경됩니다.
1.0000111₂ × 2^5[# 10 0001.11₂의 자릿수를 내렸으므로 뒤에 그만큼의 자릿수를 곱해줍니다. 이 방법을 과학적 표기법이라고 합니다.]
이진수로 표기를 마쳤으니 이 값을 메모리에 넣어야 합니다.
자료형들의 구조는 아래처럼 되어있습니다.

십진 실수를 이진수로 변환한 뒤 과학 표기법으로 만들게 되면 남은 정수 부분은 무조건 1인 것이 자명합니다. 그렇다면 우리는 굳이 정수 부분을 넣을 필요가 없습니다. 따라서 우리는 소수와 자릿수 부분만 저장하면 되겠네요. 소수 부분은 mantissa(fraction) 부분에, 자릿수는 exponent에 저장합니다.
정리하겠습니다.

양수이니 sign비트는 0이 들어갑니다.
과학 표기법으로 표기된 뒤의 소수는 0000 111[# 소수이기 때문에 뒷자리가 세 개입니다. 만일 정수였다면 000 0111이라고 작성했을 것입니다.]이므로 mantissa 영역엔 아래와 같이 작성될 것입니다.

mantissa의 길이는 float 기준으로 23개입니다. 우리는 상위 7개의 비트를 사용했습니다. 나머지 16개의 비트는 모두 0으로 값을 대입합니다.
이제 자릿수를 넣을 exponent값을 넣어주면 됩니다. 하지만 주의할 점이 있습니다. 자릿수는 항상 양수만 나오지는 않습니다. 만일 33.75가 아니라 0.75라면? 0.11₂가 나옵니다. 이를 과학 표기로 바꾸면 1.1₂ × 2^(-1)이 됩니다. 즉, 자릿수에 해당하는 값이 음수가 나올 수 있습니다. 그래서 127을 자릿수에 더해줍니다. exponent의 비트 수는 8개입니다. 최대 255까지 값을 가지므로, 그 절반인 127을 더해줍니다. 이때 더해주는 127을 bias라고 부릅니다.
# 127을 더하지 않고 2의 보수를 사용하면 안 되나요?
물론 2의 보수를 이용할 수도 있습니다. 그러나 2의 보수를 이용하는 것보다 값의 절반인 127을 더해주는 것이 연산이 더 적습니다.
자릿수가 4인 값이 있다면 우리는 2의 보수를 먼저 취할 수 있습니다.
- 자릿수 4의 이진수 값: 0100₂
- 자릿수 4의 이진수 값 반전 >> 1011₂ (1의 보수 상태)
- 반전된 값에 + 1 : 1100₂ (최종)
반전과 덧셈, 총 두 번의 연산이 이루어집니다.
그러나 255의 절반인 127을 더하는 과정은 덧셈 단 한 번이면 이루어집니다. 연산 상의 이득을 보는 것이죠.
이번 경우엔 양수인 5이므로 127에 5를 더한 132의 이진수 1000 0100을 exponent에 넣어줍니다.
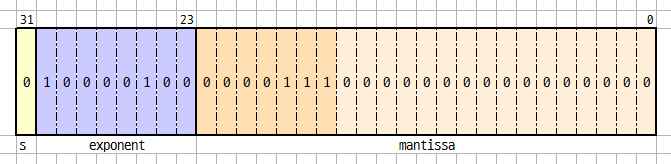
직접 작성한 float 자료형에 넣은 실수 값 33.75입니다. 이제 실제로 맞는지 비교해보도록 하겠습니다.
#include <stdio.h>
typedef union{
float origin;
struct {
unsigned int mantissa:23;
unsigned int exponent:8;
unsigned int sign:1;
}d;
}data;
int main()
{
data v;
v.origin = 33.75f;
printf("%u ", v.d.sign);
for(int i = 7; i >=0; --i){
printf("%u", (v.d.exponent & (1 << i)) != 0);
}
printf(" ");
for(int i = 22; i >=0; --i){
printf("%u", (v.d.mantissa & (1 << i)) != 0);
}
printf("\n");
return 0;
}
공간을 공유하는 union 문법과 비트 필드 연산자를 활용하면 쉽게 구분 지을 수 있습니다. 이 코드를 실행해보겠습니다.

| 만든 비트 패턴 | 0100 0010 0000 0111 0000 0000 0000 0000 |
| 프로그램에서 연산한 비트 패턴 | 0100 0010 0000 0111 0000 0000 0000 0000 |
| 일치 여부 | True |
이제 우리는 프로그램 없이도 부동 소수점의 비트를 알아낼 수 있습니다.
부동 소수점 방식을 사용하면 가장 좋은 점은 특정 수를 저장할 때 더 많은 공간이 필요한 고정 소수점 방식에 비해 작은 공간으로 많은 수를 표현할 수 있습니다.
그러나 단점 또한 존재합니다.
부동소수점은 ==으로 비교하지 마세요
말 그대로 부동 소수점, C/C++에서는 float나 double로 불리는 자료형은 == 연산자로 비교해서는 안됩니다. 그 이유를 알아봅시다. 3.14 == 3.14는 거짓일 수 있습니다. 3.14를 비교하는 코드를 보겠습니다. #incl..
pang2h.tistory.com
윗글에서 간단히 설명했듯 부동 소수점 방식은 그 특성상 오차가 발생합니다.
부동 소수점의 단점
오차
부동 소수점은 위에서 저장 방식을 설명할 때 숫자 본연의 값 그대로를 넣지 않고, 값에 대한 정보를 저장하는 방식이라고 했습니다. 그렇기 때문에 비트 자체가 값이 될 수는 없는데, 연산을 통해 실제 값을 찾아내는 방식입니다. 그러나 아래 값은 mantissa의 범위보다 더 많은 비트가 존재해야 실제 값의 정보를 모두 담을 수 있거나 나머지가 순환되어 실제 값을 저장할 수 없습니다.


1.85라는 값을 보면, 실제 값을 저장할 때 나머지의 값이 [0.8, 0.6, 0.2, 0.4]로 계속 순환되는 것을 알 수 있습니다. 결국 1.85라는 값을 저장할 수 없는 것입니다.
그래도 이 표준에서는 표준에서 "이 자릿수까지는 절대적으로 입력과 일치한다!"라고 공표한 유효자리가 존재합니다. 그래서 일정 소수까지는 마음 놓고 사용할 수 있습니다. float는 7자리, double은 15자리까지 보장합니다.
# 부동소수점의 유효자리는 없다
2021.09.01.(Wed) 추가
위에서 언급한 것과 마찬가지로 기본적인 데이터 저장 체계가 int, long 등과 같은 정수 데이터 타입과 다릅니다. 때문에 부동소수점의 유효자리는 정확하다고 볼 수 없습니다. 인터넷에 떠도는 유효자리 이야기는 아마도 가장 앞의 수와 몇자리 떨어진 수까지 같은 값을 보이는가?에 대한 내용이 아닐까 추측해봅니다.
#include <stdio.h>
int main(void) {
float f = 0.123456789;
float ft = 10000205.625456;
printf("%.17f\n", f);
printf("%.17f\n", ft);
return 0;
}이 코드로 실증을 해보면 그 결과가 아래처럼 나옵니다.

즉, 소수 몇째 자리까지의 값을 보증한다는 말은 존재하지 않는다고 볼 수 있습니다.

그러나 열 한자리까지 출력해보겠습니다.
printf("%u %u %u %.11f\n", v.d.sign, v.d.exponent, v.d.mantissa, v.origin);


비트패턴과 동일한 값이 노출됩니다. 코드에선 1.85f로 작성했지만, 비트 패턴으로 연산하니 1.8500 0002 384가 나옵니다. 스물세 개의 비트로 1.85에 가장 가까운 값을 만든 것이죠.

만일 이미지상 23번(실제 메모리 구조에선 0번) 비트가 1이 아니었다면 약 9.0 × 10^(-8)이란 값의 차이가 발생합니다. 마지막 비트를 1로 했을 때 약 7.0 × 10^(-8)만큼 더 정확한 것입니다.
비교
이렇게 저장 방식의 문제로 인해 발생하는 오차가 프로그램에서 실수의 비교에 문제를 일으키기 때문에 실수끼리의 비교는 단순히 비교 연산자인 ==을 이용하지 않고 그 둘의 차이가 충분히 작은지를 판별하도록 합니다.
Reference.
부동소수점 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 초기의 전기기계식 프로그래밍 가능한 컴퓨터 Z3에는 부동소수점 산술 기능이 포함되었다. (뮌헨의 국립 독일 박물관) 부동소수점(浮動小數點, floating point) 또는 떠돌이 소수점[1] 방식은 실수를 컴퓨터상에서 근사하여 표현할 때 소수점의 위치를 고정하지 않고 그 위치를 나타내는 수를 따로 적는 것으로, 유효숫자를 나타내는 가수(假數)와 소수점의 위치를 풀이하는 지수(指數)로 나누어 표현한다. 컴퓨터에서는 고정
ko.wikipedia.org
게임을 움직이는 수학과 물리
게임 속 움직임을 표현해주는 수학과 물리를 수학의 기본인 수부터 설명한다. 먼저 정수, 소수, 사칙연산 같은 숫자 구조와 연산을 살펴본다. 기본적인 수학 학습 이후, 2차원에 쓰는 중력, 가속도, 마찰, 3차원에 쓰는 평면, 행렬, 벡터 같은 게임 물리를 410개의 그림과 112개의 코드를 이용해 설명한다. 이 책을 읽고 나면 기본적인 게임 수학 물리를 이...
www.yes24.com
# index
'DEV > C C++' 카테고리의 다른 글
| 프로그램에 일상을 더하다: 여러 항목 정렬하기 (0) | 2020.03.19 |
|---|---|
| XOR: 배타적 논리합 (0) | 2020.02.28 |
| 포인터(pointer) part4. 함수 포인터 배열 (0) | 2020.01.30 |
| 포인터(pointer) part3. 함수 포인터 (0) | 2020.01.30 |
| 구조체(struct) part2. 비트 필드 (0) | 2020.01.29 |




